Covariance Matrices: Challenges and Pitfalls

Blog Post by Best Fin Investment

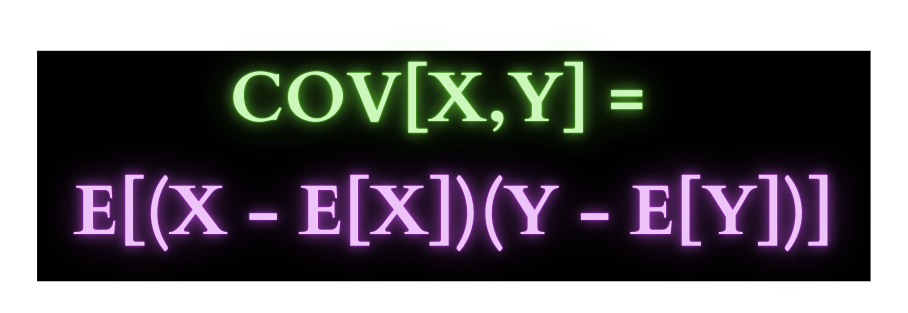
Table of Contents:

• Introduction
• Correlation Matrix versus Covariance Matrix
• Role and Significance of Covariance Matrices
• Challenges of Covariance Matrices in Real-World Portfolios
• Conclusion
• Explore Portfolio Optimization tools on the Best Fin Investment Dashboard
• References
• Related Articles
• Books from the References Section
• Additional Reading on Random Matrix Theory, the Marcenko-Pastur Equation, Covariance Matrices, and Portfolio Optimization

Introduction:
Optimal asset allocation, which entails selecting a limited number of assets from a predetermined pool to achieve optimal risk-return performance, is one of the most critical and challenging tasks in the finance industry ^[3]. Among the numerous asset allocation strategies, also known as "portfolio optimization" strategies, the mean-variance Markowitz framework ^[7] and the Global Minimum Variance Portfolio (GMVP) are commonly used in real-world asset allocation scenarios. In a wide range of asset allocation strategies, the estimation of large covariance matrices and inverse covariance matrices from relatively short time-span multivariate observations is mandatory.
Covariance matrices, in the realm of portfolio optimization, are mathematical tools used to quantify the linear relationships between different assets in a portfolio. Essentially, a covariance matrix can be seen as a collection of pairwise linear relationships between different assets, forming a representation of how the returns of one asset move in relation to the returns of other assets. In other words, a covariance matrix captures the degree to which the returns of different assets tend to move together or in opposite directions.
Now since portfolio diversification relies on the "correlations" between assets, the estimation of these relationships - encapsulated in the covariance matrix - lies at the core of risk management policies ^[2]. Accordingly, the insights provided by covariance matrices are instrumental in formulating effective asset allocation strategies that aim to maximize returns while managing risk. Unfortunately, the computation of covariance matrices is notoriously fraught with various challenges ^[8], which will be briefly reviewed in this blog.

Correlation Matrix versus Covariance Matrix:
The Pearson correlation matrix, which is used frequently in portfolio management, is a normalized form of the covariance matrix. In a correlation matrix, each element is scaled by the standard deviations of the respective variables, allowing the matrix to measure the strength and direction of linear relationships, independent of unit scales.

Role and Significance of Covariance Matrices:
Covariance matrices play a crucial role in the realm of financial frameworks:

1) In Markowitz’s seminal work on portfolio theory, which forms the cornerstone of modern portfolio management, the concept of covariance matrices is fundamental. Markowitz introduced the notion that investors can construct an optimal portfolio by considering the relationship between different assets in terms of their expected returns and volatilities. Central to this theory is the diversification of assets to reduce overall portfolio risk. Covariance matrices provide a quantitative measure of the relationships between assets, allowing investors to balance risk and return effectively ^[7].

2) Covariance matrices are also indispensable tools in risk management practices. Understanding the correlations between different asset classes and individual securities is crucial for assessing and managing portfolio risk. By quantifying the relationships between assets, covariance matrices can help identify potential sources of risk and potentially devise strategies to hedge against adverse movements in the market ^[4].

Challenges of Covariance Matrices in Real-World Portfolios:
A range of of issues surround the computation of covariance and inverse covariance matrices, including:

- Time-Instability of Covariance Matrices: Covariance matrices are not stable over time, as this instability may arise from changes in correlations but perhaps more so from fluctuations in the individual volatilities of the assets ^[2].

- Extremal Correlations: Two assets can exhibit extremal correlations (e.g., during periods of high volatility or market downturn, during a financial crisis or a sudden economic shock) while showing zero covariance during stable economic conditions. This suggests that classical covariance matrices may not fully capture the correlation of extremes. This distinction is vital as it may question the traditional reliance on sample covariance matrices for portfolio optimization ^[2] and also has implications for risk management as the probability of a large loss in a diversified portfolio is dominated by the correlated moves of the portfolio constituents ^[2].

- Inversion of Ill-Conditioned Covariance Matrices: The classical Markowitz’s portfolio optimization framework delivers optimal investment strategies. However, this optimization framework does necessitate the inversion of the covariance matrix ^[7]. In practice, when managing portfolios with hundreds or more assets, the covariance matrix may not be full rank and thus may be non-invertible if the number of time observations T is fewer than the number of portfolio assets N. In other cases, even if the covariance matrix is full rank, it may still be ill-conditioned when the number of time observations T is not large enough when compared to the number of portfolio assets N. To ensure the robust estimation of the inverse covariance matrix and to properly apply the Markowitz portfolio optimization framework as originally intended, a sufficient number of data observation points is indeed essential. Without an adequate number of observations, the covariance matrix may be ill-conditioned, leading to numerical instability and potentially erroneous optimization results. It has indeed been claimed that "for monthly return based US stock market, it was estimated that a Global Minimum Variance Portfolio (GMVP) requires a sample size larger than 6,000 months (500 years !) for a portfolio with 50 assets in order to outperform a simple Equally Weighted Portfolio (EWP)" ^[8]. This is why practitioners sometimes tend to favor robust formulas that assign equal weights to all predictor or input variables, e.g. an Equally Weighted Portfolio, as these models are not affected by so-called accidents of sampling ^[5]. Now attempting to invert an ill-conditioned large matrix can be a tedious and numerically unstable task. One solution to this challenge is the application of the so-called Moore-Penrose generalized inverse to compute the inverse covariance matrix ^[8]. While the Moore-Penrose inverse does provide a way to handle non-invertible or ill-conditioned matrices, it does not necessarily guarantee that the resulting computations are optimal from a numerical stability standpoint. The results might still be sensitive to small changes in input data, which is often a common problem in financial models dealing with high-dimensional data. Hence, the proper estimation of the inverse covariance constitutes a crucial step for a successful implementation of optimal asset allocation strategies.

- Big Data and the Curse of Dimensionality: Here we begin by highlighting that an empirical covariance matrix E (computed from observed price data) may not accurately represent the true covariance matrix C of the underlying statistical process, as the true covariance matrix C is unknown. To address this challenge, practitioners often rely on a large number of independent price measurements T, compared to the number of portfolio assets N, in order to construct an empirical estimate E of C ^[1]. As T approaches infinity with N fixed, the law of large numbers ensures that E converges to the true covariance C. However, in the context of big data, where both the sample size T and the number of variables N are very large, specific issues arise when the observation ratio q = N/T is of order unity ^[1]. This scenario, known as the high-dimensional limit or Kolmogorov regime (commonly referred to as the big data regime), presents challenges in accurately estimating covariance matrices. For instance, consider a typical portfolio with N = 500 stocks and T = 2500, equivalent to 10 years of daily data, resulting in q = 0.2. In such cases, the empirical covariance matrix E might be highly noisy, leading to significant uncertainties around its eigenvalues and eigenvectors. Consequently, E may not adequately capture the true asset correlations, potentially resulting in underestimated risk estimates, particularly in out-of-sample scenarios, i.e. underestimating future risk ^[1]. To address this issue, Random Matrix Theory (RMT) offers a fundamental result known as the Marcenko-Pastur equation, which aids in better estimating the eigenvalues of large-dimensional covariance matrices. This theoretical framework helps refine the analysis of the empirical covariance matrix E before its application in portfolio optimization ^[1]. Alternatively, factor models may also offer versatile and reliable methods for computing estimates of covariance and inverse covariance matrices ^[8].

Conclusion:
The challenges and pitfalls surrounding covariance matrices in real-world portfolios underscore the complexity of modern financial analysis. While these matrices serve as essential tools in portfolio optimization and risk management, their computation and interpretation are fraught with various challenges. From the time-instability of covariance matrices to the complexities posed by extremal correlations and ill-conditioned matrices, navigating these challenges requires a deep understanding of both financial theory and mathematical principles. Moreover, in the era of big data, where vast datasets and high-dimensional data are the norm, traditional approaches to covariance estimation may fall short. However, despite these challenges, advancements in Random Matrix Theory offer promising avenues for addressing the complexities associated with covariance matrices. By refining the estimation and interpretation of covariance matrices, we can enhance the effectiveness of portfolio optimization strategies and bolster risk management practices.

Explore Portfolio Optimization tools on the Best Fin Investment Dashboard:

• Volatility vs. Return (Convex Optimization)
• Portfolio Performance

References:

Related Articles:

• Asset Correlation: An Introduction to Basic Concepts
• Trading Strategies: From Momentum to Mean-Reversion

Books from the References Section:

Note: this site contains affiliate links, please refer to the Disclaimers for more information.

Additional Reading on Random Matrix Theory, the Marcenko-Pastur Equation, Covariance Matrices, and Portfolio Optimization:

Note: this site contains affiliate links, please refer to the Disclaimers for more information.